백준 알고리즘 No.1260 DFS와 BFS
그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오. 단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 있는 점이 없는 경우 종료한다. 정점 번호는 1번부터 N번까지이다.
입력
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사이에 여러 개의 간선이 있을 수 있다. 입력으로 주어지는 간선은 양방향이다.
출력
첫째 줄에 DFS를 수행한 결과를, 그 다음 줄에는 BFS를 수행한 결과를 출력한다. V부터 방문된 점을 순서대로 출력하면 된다.
체감 난이도: ★★★
DFS와 BFS에 대한 이론은 알고있었지만 직접 구현해본것은 처음이라 어려웠다. 하지만 이미 구현하는 법을 알고있다면 굉장히 기본적인 문제일 것이다..
Code
from collections import deque
# 재귀를 활용한 DFS 함수
def dfs(v):
dfs_visit[v] = 1 # 현재 노드 방문 처리
print(v, end=' ') # 출력
for i in range(1, n+1): # 그래프를 순회하며
if graph[v][i] == 1 and dfs_visit[i] == 0: # 인접한 노드 중 방문하지 않은 노드에 대해
dfs(i) # 함수 재귀 호출
# 큐를 활용한 BFS 함수
def bfs(v):
q = deque([v]) # 큐 선언 및 시작 노드 추가
bfs_visit[v] = 1 # 시작 노드 방문 처리
while q: # 큐가 빌 때까지 반복
v = q.popleft() # 현재 노드를 큐에서 꺼내고
print(v, end=' ') # 출력
for i in range(1, n+1): # 그래프를 순회하며
if graph[v][i] == 1 and bfs_visit[i] == 0: # 인접한 노드 중 방문하지 않은 노드를
q.append(i) # 큐에 추가 후
bfs_visit[i] = 1 # 방문 처리
n, m, v = map(int, input().split()) # 정점의 개수, 간선의 개수, 탐색을 시작할 정점
# 노드 인덱스가 1부터 시작하기에 (n+1) * (n+1)로 만들어준다.
graph = [[0] * (n+1) for _ in range(n+1)] # 2차원 행렬을 0으로 초기화
for i in range(m): # 간선의 개수만큼
a, b = map(int, input().split()) # 연결해야 하는 두 정점 입력 받기
graph[a][b] = graph[b][a] = 1 # 연결 표시
dfs_visit = [0] * (n+1) # DFS 방문 여부 리스트 초기화
bfs_visit = [0] * (n+1) # BFS 방문 여부 리스트 초기화
dfs(v)
print()
bfs(v)
Solution
우선 이 문제를 풀기 위해서는 DFS와 BFS에 대한 이해가 필요하다.
참고 영상: Click Here!
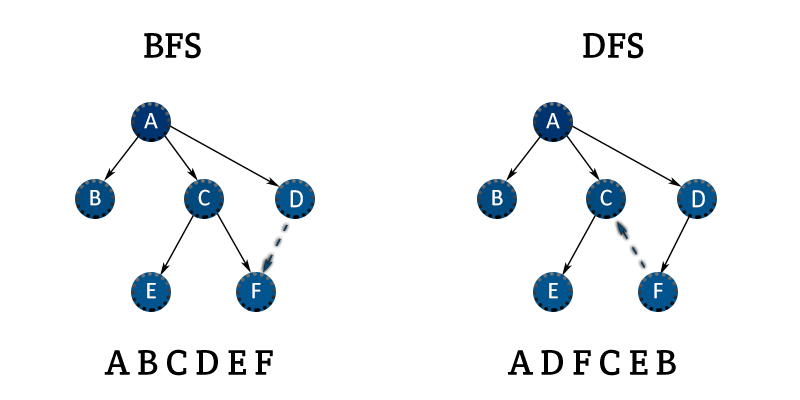
DFS (깊이 우선 탐색)
- 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘
- 주로 미로 찾기, 경로 찾기 등에서 사용
- 특정 노드에서 깊숙히 들어가서 경로를 찾을 때 유용
✔ DFS의 동작 순서
- 시작 노드를 스택 또는 재귀 호출을 통해 방문
- 현재 노드를 방문 처리하고 출력
- 현재 노드와 인접한 노드 중에서 아직 방문하지 않은 노드를 찾음
- 방문하지 않은 이웃 노드가 있으면 해당 노드로 이동하고 2번부터 반복
- 더 이상 방문하지 않은 노드가 없다면, 이전 단계로 돌아가서 다른 이웃 노드 탐색
(스택에서 pop하거나, 재귀 호출에서 반환하면서 이전 단계로 이동)- 스택이 비어 있거나, 재귀 호출이 모두 종료되면 DFS 종료
✔ DFS의 구현 방법 1 - 스택(Stack)
def dfs_stack(graph, start):
stack = [start] # 시작 노드를 스택에 추가
visited = [False] * (len(graph) + 1) # 방문 여부를 저장하는 리스트
while stack: # 스택이 빌 때까지 반복
node = stack.pop() # 현재 방문하고 있는 노드를 꺼내고
visited[node] = True # 방문 체크 후
print(node, end=' ') # 출력
# 스택에 역순으로 인접 노드를 추가
for neighbor in reversed(graph[node]): # 현재 노드와 연결된 인접 노드 중
if visited[neighbor] is False: # 방문하지 않은 노드(다음에 방문할 노드)를
stack.append(neighbor) # 스택에 추가
⭐️ DFS를 스택으로 구현할 때 역순으로 인접 노드를 추가하는 이유
- 스택에서
pop연산을 사용하면 가장 최근에 추가된 요소가 먼저 꺼내진다.- 따라서 인접한 노드들을 역순으로 스택에 추가하면
pop할 때 맨 먼저 추가된 인접 노드부터 꺼내어 탐색하게 된다.- 이를 통해 같은 레벨의 노드 중에 더 깊이 있는 노드들을 먼저 탐색하게 된다.
✔ DFS의 구현 방법 2 - 재귀(Recursive)
def dfs_recursive(graph, current_node, visited=None):
if visited is None: # 처음 호출 시에만
visited = [False] * (len(graph) + 1) # 방문 여부를 저장하는 리스트 초기화
visited[current_node] = True # 현재 노드를 방문했다고 표시
print(current_node, end=' ') # 현재 노드 출력
for neighbor in graph[current_node]: # 현재 노드와 연결된 인접 노드 중
if visited[neighbor] is False: # 방문하지 않은 노드(다음에 방문할 노드)에 대해
dfs_recursive(graph, neighbor, visited) # dfs_recursive 함수를 재귀 호출
dfs_recursive함수의 정의에서visited=None은visited파라미터가 기본값으로None을 갖는다는 것을 의미- 이렇게 하면 함수 호출 시
visited파라미터를 생략 가능if visited is None:을 통해 함수가 처음 호출될 때만 방문 여부를 저장하는 리스트가 초기화- 함수가 재귀적으로 호출 되었을 때
visited가 공유되지 않도록 하기 위함
BFS (너비 우선 탐색)
- 그래프에서 가까운 부분을 우선적으로 탐색하는 알고리즘
- 최단 경로 문제에서 많이 사용
- 레벨 단위로 탐색하기 때문에 최단 경로 보장
✔ BFS의 동작 순서
- 시작 노드를 큐에 넣고 방문 처리
- 큐에서 노드를 하나 꺼내서 방문
- 현재 노드와 인접한 노드 중에서 아직 방문하지 않은 노드를 큐에 추가하고 방문 처리
- 큐가 빌 때까지 2번과 3번 반복
- 레벨 단위로 탐색하면서, 현재 레벨의 모든 노드를 방문한 후 다음 레벨로 이동
- 모든 노드를 방문할 때까지 BFS 계속 진행
✔ BFS의 구현 방법 - 큐(Queue)
def bfs(graph, start):
queue = deque([start]) # 시작 노드를 큐에 추가
visited = [False] * (len(graph) + 1) # 방문 여부를 저장하는 리스트
while queue: # 큐가 빌 때까지 반복
node = queue.popleft() # 현재 방문하고 있는 노드를 꺼내고,
visited[node] = True # 방문 체크 후
print(node, end=' ') # 출력
for neighbor in graph[node]: # 현재 노드와 연결된 인접 노드 중
if visited[neighbor] is False: # 방문하지 않은 노드(다음에 방문할 노드)를
queue.append(neighbor) # 큐에 추가
- 스택을 활용한 DFS 알고리즘과 동작 순서는 동일하지만 큐를 쓴다는 것만 다름
- 스택을 사용하면 마지막에 추가된 노드부터 탐색하게 되어 깊이 우선 탐색에 적합
- but, 큐는 먼저 추가된 노드부터 탐색하게 되어 너비 우선 탐색에 적합
출력 결과 (DFS & BFS)
▶ Input
graph = {
1: [2, 3], # 1
2: [1, 4, 5], # / \
3: [1], # 2 3
4: [2], # | \
5: [2] # 4 5
}
▶ Output
DFS by Stack: 1 2 4 5 3
DFS by Recursive: 1 2 4 5 3
BFS: 1 2 3 4 5
💡 코드를 줄이고 싶다면?
- 인접한 노드들을
append가 아닌extend로 한번에 삽입- 리스트 컴프리헨션 문법 활용
for neighbor in graph[node]: # 현재 노드와 연결된 인접 노드 중
if visited[neighbor] is False: # 방문하지 않은 노드(다음에 방문할 노드)를
queue.append(neighbor) # 큐에 추가
# 간략화한 코드
queue.extend(neighbor for neighbor in graph[node] if not visited[neighbor])
혹시 더 좋은 알고리즘 풀이가 있다면 언제든 댓글로 알려주세요 😃
